Optimization methods are an integral part of the training process of Deep neural networks, but most are using them as black box optimizers. This occurs because lack of practical knowledge about those optimizers. Today I'll try providing some intuition on some of the more popular algorithms.

Before we dive into the different algorithms we must understand – why does "vanilla" gradient descent (i.e. stochastic gradient descent) isn't good enough?

1. Learning Rate – Choosing a good learning rate is difficult and sometimes requires optimization (grid search, etc.). On one side while using high learning rate the convergence can be hindered , but on the other side while using small learning rate the convergence might be too slow.
2. Learning schedule –Vanilla gradient descent requires us using predefined schedule or thresholds in order to use learning rate decay or any other learning schedule of our liking.
3. Updating sparse data – When we have sparse data and our features frequencies vary, we might want to update them differently, i.e. large updates for rarely occurring features.
4. Minimizing non-convex error function – Usually when optimizing a neural network, we would face the problem of avoiding sub-optimal local minima and saddle points. The bigger problem are saddle points, because they usually surrounded by a plateau, i.e. the gradient is close to zero, which makes it hard to "escape" for vanilla gradient descent.

With the aim of solving the problems above, many optimizers have been developed. Here I'd present you the most popular ones and explain what is their advantages:

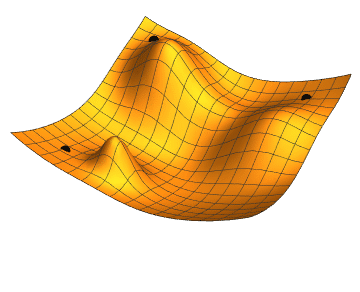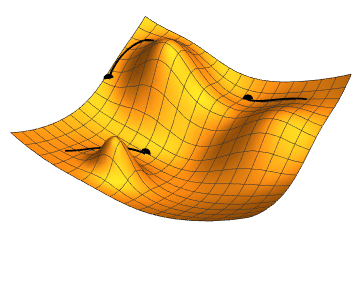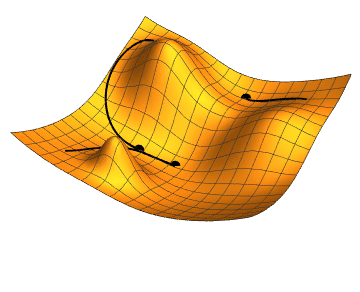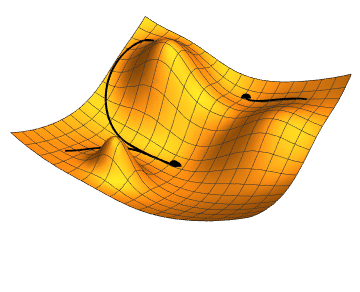
1. Momentum – SGD has problem dealing with ravines, where the surface is curving more steeply in one dimension than in the others. Vanilla gradient descent would oscillate more in a narrow ravine, because the gradient won't point along the ravine towards the optimum. This is shown in the following images:

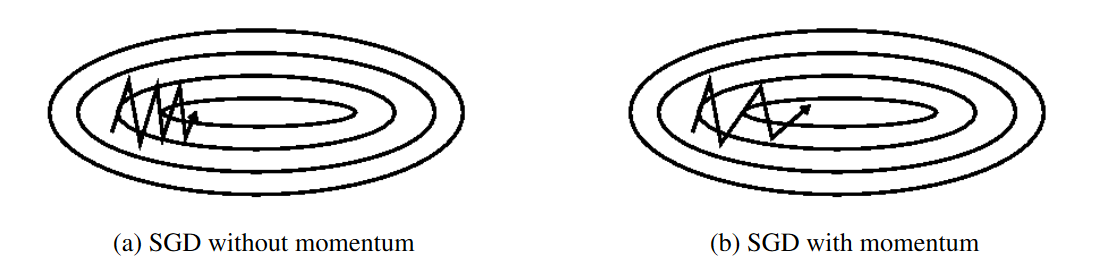
             Source: Genevieve B. Orr

To implement momentum, instead of using the derivative of the weights and bias independently for each epoch, we use exponentially weighted averages on them:

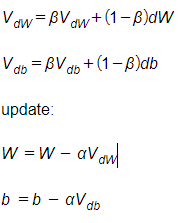
Where β is a hyper parameter called momentum and ranged from 0 to 1. The momentum term is usually set to 0.9.

2. Adagrad – This algorithm adapts the learning rate for each parameter, thus eliminating the need to manually tune the learning rate. The strength of this algorithm is that it performs larger updates for infrequent parameters and smaller updates for frequent parameters. This property helps this algorithm dealing with tasks that have sparse data. The update can be done this way because Adagrad uses a different learning rate for every parameter. The following equation explains the process (I would use the same writing to be aligned with the original article):

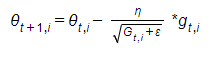
Where g is the current gradient, and G is a vector, in which every i-th element is the sum of squares of the i-th parameter gradients. ε is used in order to avoid division by zero (usually 1e-8).

Adagrad's weakness is that the accumulation of the squared gradients doesn't stop and shrink the learning rate to eventually become infinitesimally small (i.e. the algorithm stops learning).

3. RMSprop – Root mean square prop was developed by Geoff Hinton with the aim of solving Adagrad's radical diminishing learning rates. The main idea of RMSprop is using exponential moving average of the squared gradients for each weight. The implementation of RMSprop is the following:

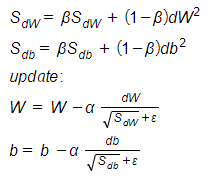
Where ε is there to ensure we won't divide by zero (usually 1e-8).

4. ADAM – Adaptive Moment Estimation is basically using the combination of RMSprop and momentum, in order to "get the best of both worlds". In ADAM we are also fixing the bias in order to lower it. All in all the implementation is the following:

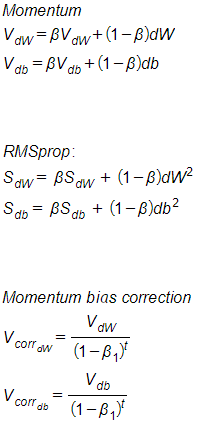
Where ε is there to ensure we won't divide by zero (usually 1e-8),  and the Betas are hyper parameters for the momentum and the squared exponential average (usually 0.9 and 0.999 respectively).

I hope that this post would help you to understand better the different optimization methods, and that you'd be able to pick the right one for your task.

Yours,

Don Shaked